前言
Python 中的 list 是一种序列类型,可以存储任意类型的对象,如整数、字符串、元组等。 list 是可变的,也就是说,我们可以在运行时添加、删除或修改 list 中的元素。那么,Python 中的 list 是如何实现和使用的呢?本文将从以下几个方面来介绍:
- list 的内部结构
- list 的动态扩容机制
- list 的时间复杂度分析
- list 的常用操作和技巧
list 的内部结构
Python 中的 list 实际上是一个数组,但不是一个普通的数组,而是一个指针数组。也就是说,list 中的每个元素都是一个指向对象的指针,而不是对象本身。这样做的好处是,list 可以存储不同类型的对象,而不需要考虑对象的大小或对齐问题。同时,这也意味着,list 中的元素并不是连续存储的,而是分散在内存中的不同位置,通过指针来连接。
下图展示了一个包含 4 个元素的 list 的内部结构:
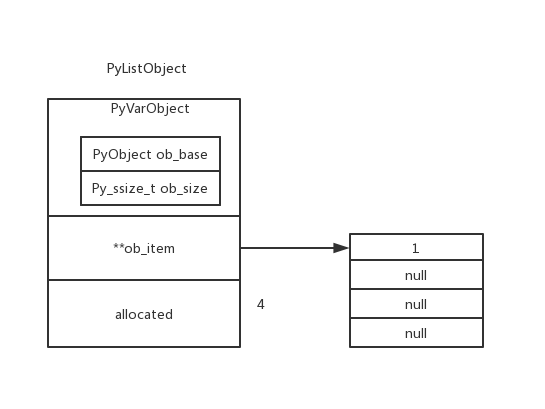
可以看到,list 对象本身有一个指向指针数组的指针,指针数组中的每个指针又指向一个对象。这样,我们可以通过 list 对象的指针,找到指针数组,再通过指针数组的索引,找到对应的对象。
list 的动态扩容机制
由于 list 是可变的,我们可以随时向 list 中添加或删除元素。那么,list 是如何管理指针数组的大小的呢?当指针数组的空间不足时,list 会自动申请更大的空间,并将原来的指针数组复制过去,然后释放原来的空间。同样,当指针数组的空间过剩时,list 会自动缩小空间,并将原来的指针数组复制过去,然后释放原来的空间。
它在 CPython 中的实现如下:
static int
list_resize(PyListObject *self, Py_ssize_t newsize)
{
PyObject **items;
size_t new_allocated, num_allocated_bytes;
Py_ssize_t allocated = self->allocated;
/* Bypass realloc() when a previous overallocation is large enough
to accommodate the newsize. If the newsize falls lower than half
the allocated size, then proceed with the realloc() to shrink the list.
*/
if (allocated >= newsize && newsize >= (allocated >> 1)) {
assert(self->ob_item != NULL || newsize == 0);
Py_SIZE(self) = newsize;
return 0;
}
/* This over-allocates proportional to the list size, making room
* for additional growth. The over-allocation is mild, but is
* enough to give linear-time amortized behavior over a long
* sequence of appends() in the presence of a poorly-performing
* system realloc().
* The growth pattern is: 0, 4, 8, 16, 25, 35, 46, 58, 72, 88, ...
* Note: new_allocated won't overflow because the largest possible value
* is PY_SSIZE_T_MAX * (9 / 8) + 6 which always fits in a size_t.
*/
new_allocated = (size_t)newsize + (newsize >> 3) + (newsize < 9 ? 3 : 6);
if (new_allocated > (size_t)PY_SSIZE_T_MAX / sizeof(PyObject *)) {
PyErr_NoMemory();
return -1;
}
if (newsize == 0)
new_allocated = 0;
num_allocated_bytes = new_allocated * sizeof(PyObject *);
items = (PyObject **)PyMem_Realloc(self->ob_item, num_allocated_bytes);
if (items == NULL) {
PyErr_NoMemory();
return -1;
}
self->ob_item = items;
Py_SIZE(self) = newsize;
self->allocated = new_allocated;
return 0;
}具体的扩缩容原理是:
- 如果目标容量
newsize小于等于原容量allocated,并且大于等于它的一半,那么不需要重新分配内存,只需要修改 list 的大小Py_SIZE为newsize。 - 如果
newsize大于allocated,或者小于它的一半,那么需要重新分配内存,根据一个公式计算新容量new_allocated,然后使用PyMem_Realloc函数重新分配内存,并更新 list 的指针ob_item,大小Py_SIZE和容量allocated。 - 如果分配内存失败,那么抛出内存错误异常。
计算新容量的公式原理是:
- 计算新容量
new_allocated。它等于newsize加上newsize的八分之一,再加上一个常数。这个常数根据newsize的大小而变化,如果newsize小于9,那么常数是3,否则是6。 - 检查
new_allocated是否超过了PyObject指针的最大值。如果是,那么抛出内存错误异常。 - 如果
newsize是0,则将new_allocated设置为 0。
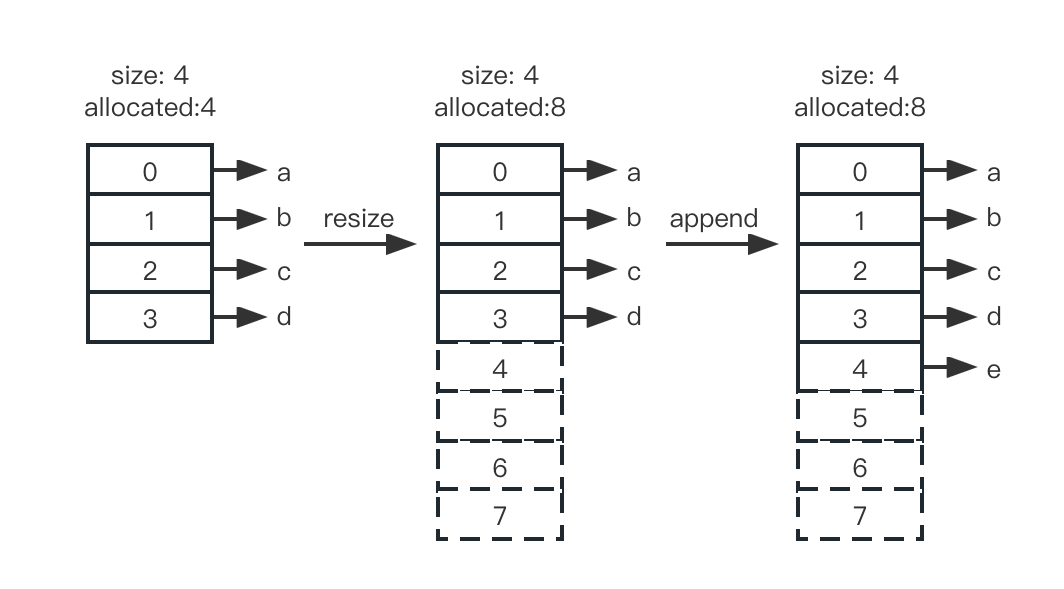
以 list 的 append() 函数为例介绍扩容过程,当 list 中有四个元素时,allocated 是 4,指针数组的空间刚好够用。当我们向 list 中添加第五个元素时,指针数组的空间不足,需要扩容。根据公式,新容量为 4+4*1/8+3=7.5,取整为 8,list 会申请一个大小为 8 的新指针数组,并将原来的指针数组复制过去,添加新元素,并释放原来的空间。
list 的时间复杂度分析
由于 list 的内部结构和动态扩容机制,list 的不同操作的时间复杂度也不同。一般来说,我们可以根据操作的类型,将 list 的操作分为以下几类:
-
索引操作:通过索引访问或修改 list 中的元素,如
lst[i]或lst[i] = x。这类操作的时间复杂度是O(1),也就是常数时间,因为我们只需要通过 list 对象的指针,找到指针数组,再通过索引,找到对应的对象,这些操作都是固定的,和 list 的大小无关。 -
追加操作:在 list 的末尾添加一个元素,如
lst.append(x)。这类操作的时间复杂度是 O(1),也就是常数时间,因为我们只需要在指针数组的末尾,添加一个指向对象的指针,这个操作也是固定的,和 list 的大小无关。当然,如果指针数组的空间不足,需要扩容,那么这个操作的时间复杂度就会变成 O(n),也就是线性时间,因为我们需要申请一个新的指针数组,并将原来的指针数组复制过去,这些操作都和 list 的大小成正比。但是,由于 list 的增长因子的存在,扩容的次数是有限的,而且随着 list 的大小的增加,扩容的频率会降低,所以我们可以认为,追加操作的平均时间复杂度仍然是 O(1),也就是常数时间。 -
插入操作:在 list 的任意位置插入一个元素,如
lst.insert(i, x)。这类操作的时间复杂度是 O(n),也就是线性时间,因为我们需要在指针数组的指定位置,插入一个指向对象的指针,这意味着,我们需要将该位置之后的所有指针,都向后移动一位,这些操作都和 list 的大小成正比。当然,如果指针数组的空间不足,需要扩容,那么这个操作的时间复杂度就会变成 O(n),也就是线性时间,因为我们需要申请一个新的指针数组,并将原来的指针数组复制过去,这些操作都和 list 的大小成正比。所以,插入操作的平均时间复杂度仍然是 O(n),也就是线性时间。 -
删除操作:从 list 的任意位置删除一个元素,如
lst.pop(i)或del lst[i]。这类操作的时间复杂度也是O(n),也就是线性时间,因为我们需要在指针数组的指定位置,删除一个指向对象的指针,这意味着,我们需要将该位置之后的所有指针,都向前移动一位,这些操作都和 list 的大小成正比。当然,如果指针数组的空间过剩,需要缩容,那么这个操作的时间复杂度也会变成 O(n),也就是线性时间,因为我们需要申请一个新的指针数组,并将原来的指针数组复制过去,这些操作都和 list 的大小成正比。所以,删除操作的平均时间复杂度仍然是 O(n),也就是线性时间。 -
遍历操作:遍历 list 中的所有元素,如
for x in lst或list(lst)。这类操作的时间复杂度也是 O(n),也就是线性时间,因为我们需要访问指针数组中的每个指针,再通过指针访问对应的对象,这些操作都和 list 的大小成正比。
从上面的分析可以看出,list 的不同操作的时间复杂度有所不同。一般来说,索引和追加操作是最快的,插入和删除操作是最慢的,遍历操作是中等的。所以,当我们使用 list 时,应该尽量避免在 list 的中间或开头插入或删除元素,而是尽量在 list 的末尾追加或删除元素,这样可以提高 list 的性能。
list 的常用操作和技巧
除了上面介绍的基本操作,list 还有一些常用的操作和技巧,可以让我们更方便地使用 list 。下面列举了一些常用的操作和技巧,以及它们的示例代码:
- 切片操作:通过指定起始和结束的索引,以及可选的步长,来获取 list 的一部分,如
lst[start:end:step]。这个操作会返回一个新的 list ,不会修改原来的 list 。示例代码:
lst = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sub_lst = lst[2:8:2] # 从索引 2 开始,到索引 8 结束,步长为 2,获取 list 的一部分
print(sub_lst) # [3, 5, 7]-
列表推导式:通过一行代码,根据一个已有的 list,生成一个新的 list,如
[x * 2 for x in lst]。这个操作可以让我们更简洁地创建 list,而不需要使用循环或追加操作。示例代码:lst = [1, 2, 3, 4, 5] new_lst = [x * 2 for x in lst] # 根据 lst 中的每个元素,生成一个新的 list,每个元素都乘以 2 print(new_lst) # [2, 4, 6, 8, 10] -
排序操作:通过指定一个排序规则,来对 list 中的元素进行排序,如
lst.sort(key=lambda x: x[1]),key 选填。这个操作会修改原来的 list ,如果不想修改原来的 list ,可以使用sorted(lst, key=lambda x: x[1]),这个操作会返回一个新的 list 。示例代码:
lst = [(1, 3), (2, 5), (3, 4), (4, 2), (5, 1)]
lst.sort(key=lambda x: x[1]) # 根据 lst 中的每个元素的第二个值,对 list 进行排序
print(lst) # [(5, 1), (4, 2), (1, 3), (3, 4), (2, 5)]-
反转操作:通过指定一个反转标志,来对 list 中的元素进行反转,如lst.reverse()。这个操作会修改原来的 list,如果不想修改原来的 list ,可以使用reversed(lst),这个操作会返回一个反转的迭代器。示例代码:
lst = [1, 2, 3, 4, 5] lst.reverse() # 反转 list 中的元素 print(lst) # [5, 4, 3, 2, 1] -
拼接操作:通过使用加号或乘号,来对 list 进行拼接,如
lst1 + lst2或lst * 3。这个操作会返回一个新的 list,不会修改原来的 list。示例代码:lst1 = [1, 2, 3] lst2 = [4, 5, 6] new_lst = lst1 + lst2 # 将 lst1 和 lst2 拼接成一个新的 list print(new_lst) # [1, 2, 3, 4, 5, 6] new_lst = lst1 * 3 # 将 lst1 重复三次,拼接成一个新的 list print(new_lst) # [1, 2, 3, 1, 2, 3, 1, 2, 3] -
拆分操作:通过使用星号,来对 list 进行拆分,如x, *y, z = lst。这个操作可以让我们更方便地获取 list 中的某些元素,而不需要使用索引或切片。示例代码:
lst = [1, 2, 3, 4, 5] x, *y, z = lst # 将 lst 中的第一个元素赋值给 x,最后一个元素赋值给 z,中间的元素赋值给 y print(x) # 1 print(y) # [2, 3, 4] print(z) # 5
总结
list 是 Python 中最常用的数据结构之一,了解它的内部结构和动态扩容机制,可以让我们更好地理解和使用 list 。同时,掌握 list 的时间复杂度分析,可以让我们更高效地编写代码。最后,熟练 list 的常用操作和技巧,可以让我们更简洁和优雅地处理数据。